20. marca americko-kanadský matematik Robert Langlands získal Abelovu cenu, za celoživotné úspechy v matematike. Langlandsov výskum ukázal, ako by koncepty z geometrie, algebry a analýzy mohli mať spoločnú väzbu na prvočísla.
Keď v máji nórsky kráľ bude odovzdávať ocenenie Langlandsovi, bude oceňovať najposlednejšiu snahu počas 2 300-ročného úsilia porozumieť kúzelným prvočíslam, pravdepodobne v matematike najväčšej a najstaršej skupine čísel.
História prvočísel ako aj posledné pokroky sú fascinujúcim príbehom. A prečo už tisícky rokov zaujímali a stále zaujímajú matematikov?
Ako nájsť prvočísla
Na štúdium prvočísel matematici už od nepamäti preosievajú celé čísla rôznymi virtuálnym sieťami až kým zostanú len prvočísla. Tento proces preosievania vytvoril už v 19. storočí tabuľky miliónov prvočísel. Dnešné počítače môžu nájsť miliardy prvočísel za menej ako jednu sekundu. Avšak hlavná myšlienka sita sa za viac ako 2000 rokov nezmenila.
„Prvočíslo je to, čo je merané samotnou jednotkou,“ napísal matematik Euklides v roku 300 p.n.l. To znamená, že provočísla nemôžu byť rovnomerne rozdelené na nejaké menšie množstvá, s výnimkou 1. Podľa konvencie, matematici nepočítajú 1 samú o sebe za prvočíslo.
Euklides dokázal nekonečnosť prvočísel, skr. že pokračujú bez prestania. Podľa histórie Eratosthenes nám dal sito, aby sme mohli prvočísla rýchlo vyselektovať. Inými slovami poskytol nám jednoduchý algoritmus ako prvočísla prakticky nájsť.
Myšlienka tohto starovekého algoritmu – Eratosthenovho sita – je nasledovná. Najprv vyfiltrujte násobky 2, potom násobky 3, potom 5 a potom 7 – prvé štyri provočísla. Ak to urobíte so všetkými číslami od 2 do 100, zostanú len prvočísla.
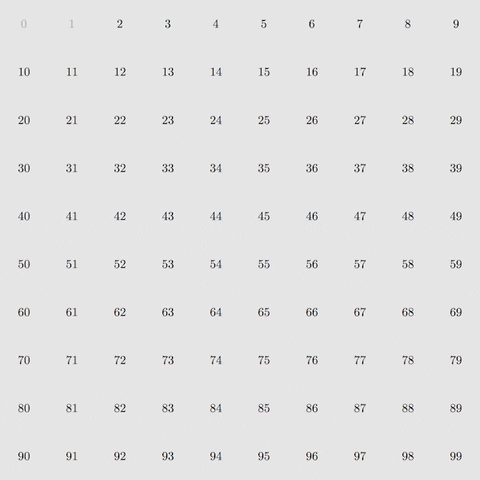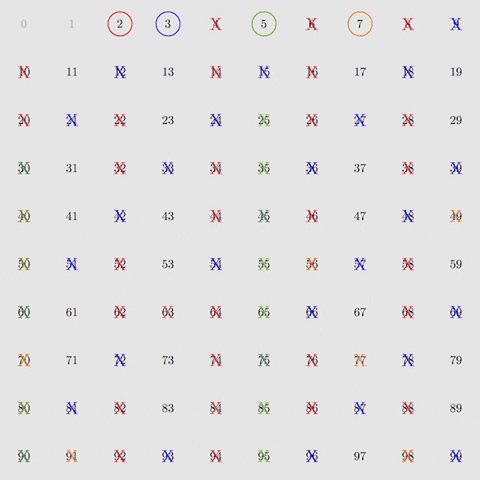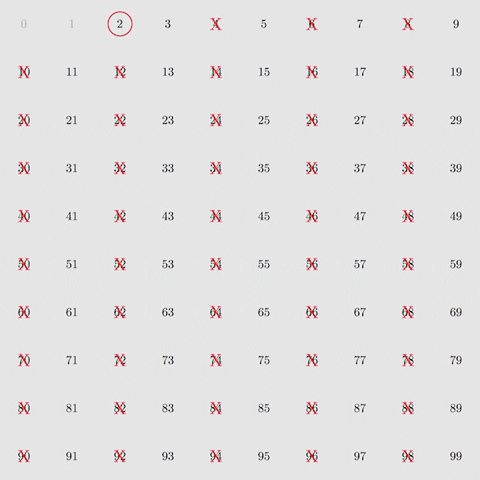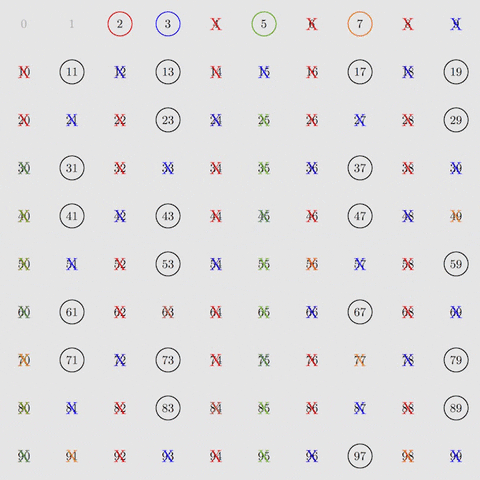
Zdroj: GIPHY
S ôsmimi filtračnými krokmi je možné izolovať prvočísla až do 400. V 168 krokoch filtrovania je možné izolovať provočísla až do 1 milióna. To je sila Eratosthenesovho sita.
Tabuľky a tabuľky
Rannou postavou v tabelovaní prvočísel je John Pell, anglický matematik, ktorý sa venoval vytváraniu tabuliek užitočných čísel. Okrem iného sa usiloval riešiť staroveké Diofantove aritmetické problémy a vďaka jeho úsiliu sme do začiatku 1700 provočísla rozšírili až na 100 000. Do roku 1800 rôzne ďaľšie nezávislé projekty tabelovali prvočísla až do 1 milióna.
Na automatizáciu únavných krokov preosievania nemecký matematik Carl Friedrich Hindenburg použil nastaviteľné posúvače, tak aby naraz eliminoval násobky na celej strane. Ďalšou malou technikou, ale efektívnou, sa stali šablóny na nájdenie násobkov. V polovici 18. storočia sa matematik Jakob Kulik pustil do ambiciózneho projektu nájsť všetky privočísla až do 100 miliónov.
Tieto „big data“ z 18. storočia mohli slúžiť iba ako referenčná tabuľka, ak by sa vynikajúci matematik Carl Friedrich Gauss nerozhodol, kvôli svojim dôvodom, prvočísla analyzovať. Vyzbrojený zoznamom prvočísel až do 3 miliónov, Gauss ich začal počítať, jeden „chiliad“, alebo skupina 1 000 jednotiek, naraz. Spočítal prvočísla až do 1 000, potom prvočísla medzi 1 000 a 2 000, potom medzi 2 000 a 3000, a tak ďalej.
Gauss zistil, že podľa toho, čo sa počíta vyššie, sa prvočísla postupne stávajú menej častými podľa „inverse-log“zákona. Gaussov zákon nekonkretizuje presne to, koľko je prvočísel, ale dáva celkom dobrý odhad. Napríklad jeho zákon predpovedá 72 prvočísel medzi 1 000 000 a 1 100 000. Správny počet je 75 prvočísel, čo je približne 4% chyba.
Storočie po prvých Gaussových bádaniach bol jeho zákon dokázaný v „teoréme o prvočíslach“. Percento chyby sa blíži k nule pri väčších a väčších rozsahoch prvočísel. Riemannova hypotéza, v súčasnosti známa ako jeden z problémov tísicročia, tiež popisuje presnosť Gaussovho odhadu. Prvočísla a Riemannova hypotéza priťahujú pozornosť i peniaze, ale obe nasledovali už skoršiu a menej očarujúcu analýzu dát.
Moderné záhady prvočísel
V súčasnosti naše súbory dát pochádzajú skôr z počítačových programov než z ručne vyrobených šablón, ale aj dnes matematici stále nachádzajú v prvočíslach nové „pattern-y“.
Okrem čísel 2 a 5 sa všetky prvočísla končia číslicou 1, 3, 7 alebo 9. V osemdesiatych rokoch sa ukázalo, že tieto posledné číslice sú rovnako časté. Inými slovami, ak sa pozriete na čísla provočísel až do jedného milióna, potom približne 25 percent končí na konci 1, 25 percent na 3, 25 percent na 7 a 25 na 9.
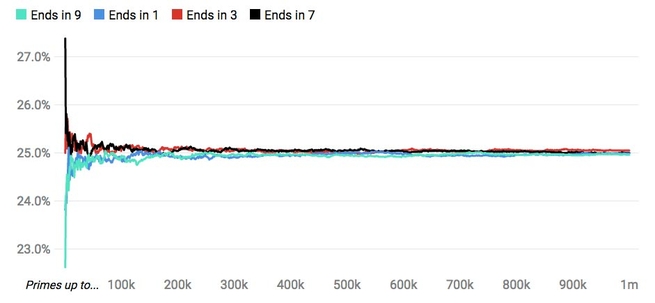
Zdroj: Úplný graf nájdete tu: The Conversation, CC-BY-ND
Pred niekoľkými rokmi stanfordskí matematici Lemke Oliver a Kannan Soundararajan objavili jednoduchú, predtým nepovšimnutú vlastnosť prvočísel. ných čísel – tie čísla, ktoré sú deliteľné iba 1 a sami. V experimente sa pozreli na poslednú číslicu prvočísla, rovnako ako na poslednú číslicu najbližšieho provočísla. Napríklad nasledujúci provčíslo po 23 je 29: vidíme, že 3 a 9 (3 potom 9) sú posledné číslice. Sú 3, potom 9 častejšie ako 3 a potom 7, medzi posledné číslicami prvočísel?

Matematici očakávali nejaké rozdiely, ale ich zistenia ďaleko presiahli očakávania. Provočísla sú oddelené rôznymi medzerami; napríklad medzi 23 a 29 je šesť čísel. Ale prípady „3 potom 9“ provočísel ako 23 a 29 sú oveľa bežnejšie ako prípady „7 potom 3“ prvočísel, hoci oba prípady majú rovnakú 6 medzeru.
Matematici čoskoro našli prijateľné vysvetlenie. Ale pokiaľ ide o štúdium po sebe idúcich prvočísel, väčšinou sú matematici limitovaní analýzou dát a presviedčaním. Zdá sa, že dôkazy – pre matematikov zlatý štandard, ktorý vysvetľuje, prečo sú veci pravdivé – sú na desaťročia vzdialené.



























